Hadamard Attentions: The Mighty Attentions Optimized
Attention is the mightiest layer so far, which symbolizes its parent paper that “Attention is all you need” in true sense. Almost all tasks, be it images, voice, text, reasoning, etc, uses attentions now.
But the layer is very heavy with most of STOA tasks taking days to train. Do we “really” need so many parameters to learn the intuition behind the Attention?
We discuss this below. and propose a lower Rank Hadamard attention.
Attention As Described.
Attention is described in its true form as
\[softmax(Q.K^T).V\]while it is implemented as
\[softmax([Q.W_q].[W_k^T.K^T]).[V.W_v]\]Now if we consider Q, K, V coming from the same matrix of size $m x n$ of seq length $m$ and embedding dimension $n$. And we need to assume a dimension of attention projection lets say that is $l$
Now the dimension of the multiplication is as follows
\[dim(W_q) = dim(W_k) = dim(W_v) = n \times l\] \[dim(Q) = dim(K) = dim(V) = m \times n\]Matrix multiplication for attention then now is
\[softmax(m \times n.n \times l.l \times n.n \times m).m \times n.n \times l\]which simplifies to
\[softmax(m \times m).(m \times n).(n \times l)\]this totals to $3(n \times l)$ weights. 2 times for the softmax part just to estimate a m X m matrix. which is seq_len X seq_len. We don’t have to multiply or have so many weights.
Fixed Attention.
I propose having a $m \times m$ matrix to estimate attention, which is similar to a feedforward matrix with softmax. Softmax plays the key attention part here to stress on certain inputs. After all, this is the intuition behind the attentions.
Proposed Fixed Attention
\[softmax((W_{attention})_{m \times m}).V\]Pros
- Lesser Weights.
- Faster training.
- Not Usefull when input independent attention but strictly position dependent attention works fine with this. for example $x_{t+1} = k_0 * x_{t} + k_1 * x_{t-1} + k_2 * x_{t-2}$
Cons
- Only works when attention is independent of the input.
- Not always useful. except for rearranging the input.
Hadamard Attention.
There has been recent work in optimizing attention, Synthesizer and Linformer, proving the attention matrix is low rank. Existing work proves low rank and takes a different route to optimize attention we propose replacing dot product attention(weights heavy) with Hadamard attention.
\[softmax((W_{attention})_{m \times m} * (Q.K^T)_{m \times m}).V\]Hadamard Attentions is constrained on weights and still input dependent. This optimizes the learning power of the model as we are using far fewer weights than in the original version. But do we always need so many weights, we discuss this in the results sections later.
Pros
- Lesser Weights.
- Faster training.
- Even usefull for input depndent attention like language, but assume that dot.
Cons
- Assumption here is that $m « n $, if m is comparable to n then $m \times m$ weight matrix can be larger than $n \times n$. And we may have more weights than original attention.
- The assumption, Head will take care of alternate attentions representations required.
Empirical Results
Experiment Setup
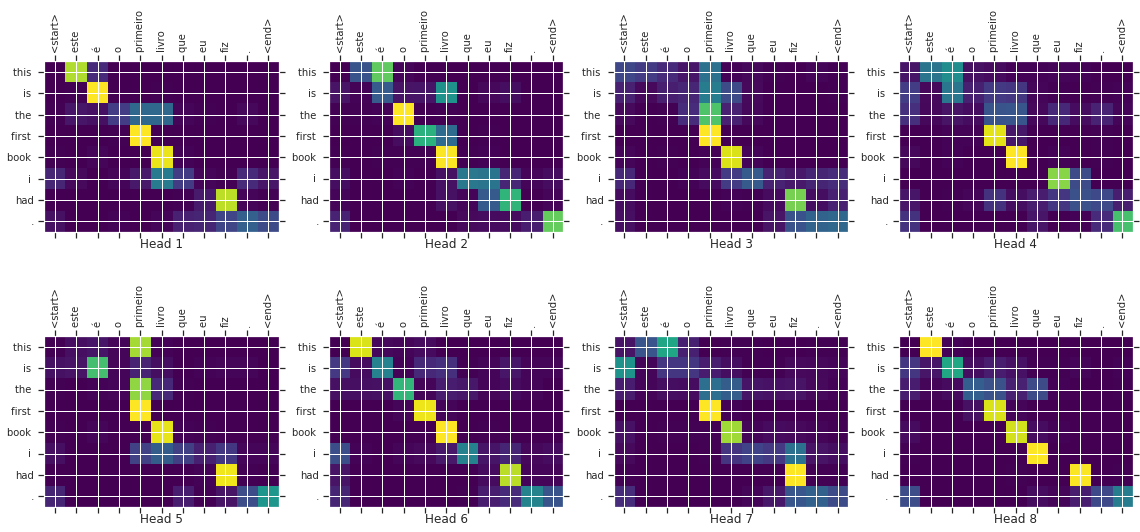
For quick analysis, we choose a language translation task as setup in the tutorial on TensorFlow attentions described here. It setups a Transformer model to translate Portuguese to English with dot product attentions. We would keep the experiment setup the same with changes only in Multi-Head Attentions Code.
Existing MultiHeadAttention code snippet from the blog can be found here
We implement a HadamardHead Layer as described below(its a modification of the original dense layer).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
from tensorflow.python.framework import dtypes
from tensorflow.python.framework import tensor_shape
from tensorflow.python.keras import backend as K
from tensorflow.python.keras import constraints
from tensorflow.python.keras import initializers
from tensorflow.python.keras import regularizers
from tensorflow.python.keras.engine.base_layer import Layer
from tensorflow.python.ops import gen_array_ops
from tensorflow.python.ops import gen_math_ops
class Hadamard(Layer):
"""Hadamard NN Layer"""
def __init__(self,
units,
kernel_initializer='glorot_uniform',
kernel_regularizer=None,
activity_regularizer=None,
kernel_constraint=None,
**kwargs):
if 'input_shape' not in kwargs and 'input_dim' in kwargs:
kwargs['input_shape'] = (kwargs.pop('input_dim'),)
super(Hadamard, self).__init__(
activity_regularizer=regularizers.get(activity_regularizer), **kwargs)
self.units = int(units) if not isinstance(units, int) else units
self.kernel_initializer = initializers.get(kernel_initializer)
self.kernel_regularizer = regularizers.get(kernel_regularizer)
self.kernel_constraint = constraints.get(kernel_constraint)
self.supports_masking = True
def build(self, input_shape):
dtype = dtypes.as_dtype(self.dtype or K.floatx())
if not (dtype.is_floating or dtype.is_complex):
raise TypeError('Unable to build `Hadamard` layer with non-floating point '
'dtype %s' % (dtype,))
input_shape = tensor_shape.TensorShape(input_shape)
if tensor_shape.dimension_value(input_shape[-1]) is None:
raise ValueError('The last dimension of the inputs to `Hadamard` '
'should be defined. Found `None`.')
last_dims = tensor_shape.dimension_value(input_shape[1:])
# if tensor_shape.dimension_value(input_shape[-1]) is None:
# heads_shape = tensor_shape.TensorShape([None, None])
# else:
heads_shape = tensor_shape.TensorShape([1, self.units])
weights_shape = heads_shape.concatenate(last_dims)
self.kernel = self.add_weight(
'kernel',
shape=weights_shape,
initializer=self.kernel_initializer,
regularizer=self.kernel_regularizer,
constraint=self.kernel_constraint,
dtype=self.dtype,
trainable=True)
self.built = True
def call(self, inputs):
return gen_math_ops.mul(gen_array_ops.expand_dims(inputs, 1), self.kernel)
def compute_output_shape(self, input_shape):
input_shape = tensor_shape.TensorShape(input_shape)
if tensor_shape.dimension_value(input_shape[-1]) is None:
raise ValueError(
'The innermost dimension of input_shape must be defined, but saw: %s'
% input_shape)
last_dims = tensor_shape.dimension_value(input_shape[1:])
batch_dim = input_shape[0]
output_shape = batch_dim.concatenate(self.units).concatenate(last_dims)
return output_shape
def get_config(self):
config = {
'units': self.units,
'kernel_initializer': initializers.serialize(self.kernel_initializer),
'kernel_regularizer': regularizers.serialize(self.kernel_regularizer),
'activity_regularizer':
regularizers.serialize(self.activity_regularizer),
'kernel_constraint': constraints.serialize(self.kernel_constraint),
}
base_config = super(Hadamard, self).get_config()
return dict(list(base_config.items()) + list(config.items()))
And MultiHadamardHeadAttention is implemented as
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
class MultiHadamardHeadAttention(tf.keras.layers.Layer):
def __init__(self, d_model, num_heads):
super(MultiHadamardHeadAttention, self).__init__()
self.num_heads = num_heads
self.d_model = d_model
assert d_model % self.num_heads == 0
self.depth = d_model // self.num_heads
self.wv = tf.keras.layers.Dense(d_model)
self.hadamard_heads = Hadamard(self.num_heads)
self.scale = self.add_weight(name='scale', shape=(),
initializer=tf.keras.initializers.Ones(),
dtype=self.dtype, trainable=True)
self.dense = tf.keras.layers.Dense(d_model)
def split_heads(self, x, batch_size):
"""Split the last dimension into (num_heads, depth).
Transpose the result such that the shape is (batch_size, num_heads, seq_len, depth)
"""
x = tf.reshape(x, (batch_size, -1, self.num_heads, self.depth))
return tf.transpose(x, perm=[0, 2, 1, 3])
def hadamard_attention(self, q, k, v, mask):
# matmultiplication
qk_T = tf.matmul(q, k, transpose_b=True) # (batch_size, seq_len, seq_len)
hadamard_heads_output = self.hadamard_heads(qk_T) # (batch_size, num_heads, seq_len, seq_len)
# scale QKT
scaled_attention_logits = hadamard_heads_output / self.scale
# add the mask to the scaled tensor.
if mask is not None:
scaled_attention_logits += (mask * -1e9)
# softmax is normalized on the last axis (seq_len_k) so that the scores
# add up to 1.
attention_weights = tf.nn.softmax(scaled_attention_logits, axis=-1) # (..., seq_len_q, seq_len_k)
output = tf.matmul(attention_weights, v) # (..., seq_len_q, depth_v)
return output, attention_weights
def call(self, v, k, q, mask):
batch_size = tf.shape(q)[0]
v = self.wv(v) # (batch_size, seq_len, d_model)
v = self.split_heads(v, batch_size) # (batch_size, num_heads, seq_len_v, depth)
# scaled_attention.shape == (batch_size, num_heads, seq_len_q, depth)
# attention_weights.shape == (batch_size, num_heads, seq_len_q, seq_len_k)
scaled_attention, attention_weights = self.hadamard_attention(q, k, v, mask)
scaled_attention = tf.transpose(scaled_attention,
perm=[0, 2, 1, 3]) # (batch_size, seq_len_q, num_heads, depth)
concat_attention = tf.reshape(scaled_attention,
(batch_size, -1, self.d_model)) # (batch_size, seq_len_q, d_model)
output = self.dense(concat_attention) # (batch_size, seq_len_q, d_model)
return output, attention_weights
Another change in the experiment setup is fixed-length input.
Weights Optimization
For embedding_size(d_model):512 and seq_len:40 we see a drop in parameter of the model from 1,050,624 to 538,113 which is a 50% drop in parameters.
We run the experiment for 50 epochs to compare in loss and accuracy. And the results are as below.
Accuracy Comparision:
We observer that there is a minimal loss in accuracy as compared to dot product attention. With dot-attention peak accuracy @37.29% hadamard score a 36.30%

We can choose another experiment setup for comparison, but the goal of the demonstration is to show minimal impact in training and saving on parameters.
Conclusion
I am not proposing against dot product attention, instead, we can carefully choose one over the other when required. Also, language models can be trained as a mix of Hadamard and Dot Product Attentions.
